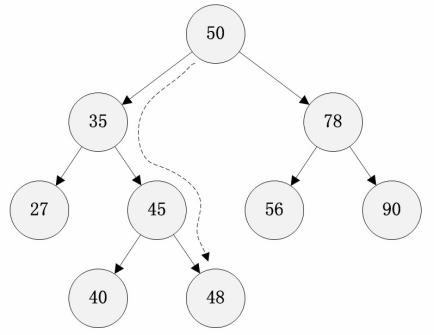
TreeMap源码解析 一、TreeMap数据结构介绍 1.红黑树简介 红黑树是一种常用的数据结构,它使得对数据的搜索、插入和删除操作都保持O(lgn)的时间复杂度
根节点必须是黑色的
任意从根到叶子的路径不包含连续的红色节点
任意从根到叶子的路径黑色节点总数相同
这些约束强制了红黑树的关键性质:从根到叶子最长的可能路径不多于最短的可能路径的两倍长.结果是这棵树大致上是平衡的.因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树.所以红黑树它是复杂而高效的,其检索效率O(lg n)
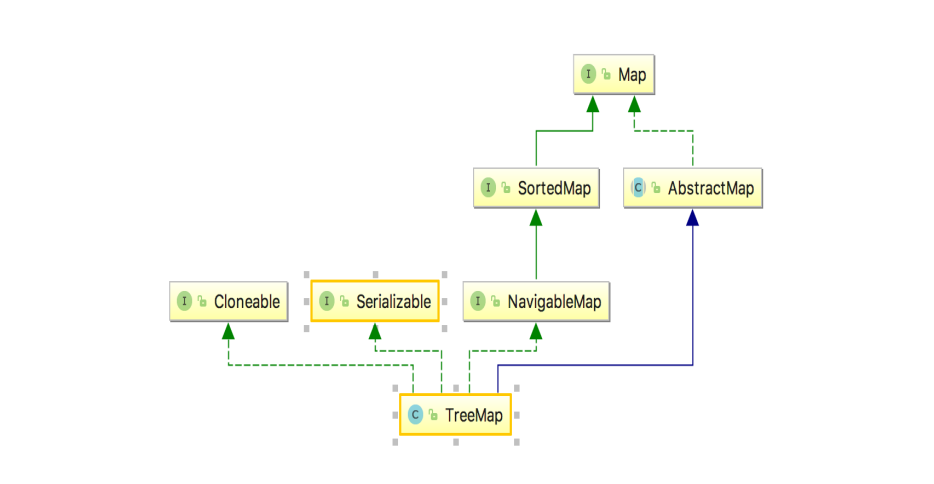
二、TreeMap的继承关系 下面先让我们来看一下TreeMap的继承关系,对它有一个大致的了解:
1.SortedMap接口源码分析 1.1SortedMap接口 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public interface SortedMap <K ,V > extends Map <K ,V > Comparator<? super K> comparator(); SortedMap<K,V> subMap (K fromKey, K toKey) ; SortedMap<K,V> headMap (K toKey) ; SortedMap<K,V> tailMap (K fromKey) ; K firstKey () ; K lastKey () ; Set<K> keySet () ; Collection<V> values () ; Set<Map.Entry<K, V>> entrySet(); }
SortedMap的接口比较简单,没有很特别的地方,唯一比较特别的就是Comparator接口,可以设想实现排序功能就在此处
1.2Comparable接口 接口代码如下:
1 2 3 4 public interface Comparable <T > public int compareTo (T o) }
里面传入一个泛型T的对象o,对o进行比较.如果小于o返回负数;等于0返回0;大于o返回正数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 @Data public class Item implements Comparable <Item > private String name; private int price; public Item (String name, int price) this .name = name; this .price = price; } @Override public String toString () return "Item{" + "name='" + name + '\'' + ", price=" + price + '}' ; } @Override public int compareTo (Item o) if (this .name.compareTo(o.name) < 0 ) { return -1 ; } else if (this .name.compareTo(o.name) > 0 ) { return 1 ; } else { return 0 ; } } public static void main (String[] args) List<Item> items = Arrays.asList(new Item("banana" , 200 ), new Item("apple" , 400 )); System.out.println("before = " + items); Collections.sort(items); System.out.println("after = " + items); } }
上述例子中,我们自己实现了Comparable接口,比较了Item的name属性,然后通过Collections.sort对它进行了排序(值得注意的是:没有实现Comparable接口的对象不能使用该方法 ).但是如果我不想用name属性对它进行排序,想对price进行排序,或者先对name排序相同在对price排序?这个时候需要Comparator接口
1.3Comparator接口 先看一下接口的源码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 @FunctionalInterface public interface Comparator <T > int compare (T o1, T o2) boolean equals (Object obj) default Comparator<T> reversed () return Collections.reverseOrder(this ); } default Comparator<T> thenComparing (Comparator<? super T> other) Objects.requireNonNull(other); return (Comparator<T> & Serializable) (c1, c2) -> { int res = compare(c1, c2); return (res != 0 ) ? res : other.compare(c1, c2); }; } public static <T> Comparator<T> comparingInt (ToIntFunction<? super T> keyExtractor) { Objects.requireNonNull(keyExtractor); return (Comparator<T> & Serializable) (c1, c2) -> Integer.compare(keyExtractor.applyAsInt(c1), keyExtractor.applyAsInt(c2)); } public static <T extends Comparable<? super T>> Comparator<T> naturalOrder () { return (Comparator<T>) Comparators.NaturalOrderComparator.INSTANCE; } }
一起来看一下如何使用,先来看一下JDK1.8之前的用法:
1 2 3 4 5 6 7 8 9 10 11 12 public class SimpleComparator implements Comparator <Item > @Override public int compare (Item o1, Item o2) return o1.price - o2.price; } public static void main (String[] args) List<Item> items = Arrays.asList(new Item("banana" , 200 ), new Item("apple" , 400 ), new Item("Orange" , 100 )); Collections.sort(items, new SimpleComparator()); System.out.println(items); } }
JDK1.8以前的用法是要自己手动实现Comparator接口,然后调用Collections.sort()传入实现类来完成排序,非常麻烦,而JDK1.8则相对来说简单了很多:
1 2 3 4 5 public static void main (String[] args) List<Item> items = Arrays.asList(new Item("banana" , 200 ), new Item("apple" , 400 ), new Item("Orange" , 100 )); Collections.sort(items, (Item a, Item b) -> a.price - b.price); System.out.println(items); }
甚至我们可以不使用Collections.sort:
1 2 3 4 5 6 7 8 public static void main (String[] args) List<Item> items = Arrays.asList(new Item("banana" , 100 ), new Item("Orange" , 100 ), new Item("apple" , 400 ), new Item("Orange" , 50 )); items.sort((Item a, Item b) -> a.price - b.price); System.out.println(items); items.sort(Comparator.comparing(Item::getName).thenComparing(Comparator.comparingInt(Item::getPrice))); System.out.println("after using thenComparing: " + items); }
1.4NavigableMap接口源码解析 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public interface NavigableMap <K ,V > extends SortedMap <K ,V > Map.Entry<K,V> lowerEntry (K key) ; K lowerKey (K key) ; Map.Entry<K,V> floorEntry (K key) ; K floorKey (K key) ; Map.Entry<K,V> ceilingEntry (K key) ; K ceilingKey (K key) ; Map.Entry<K,V> higherEntry (K key) ; K higherKey (K key) ; Map.Entry<K,V> firstEntry () ; Map.Entry<K,V> lastEntry () ; Map.Entry<K,V> pollFirstEntry () ; Map.Entry<K,V> pollLastEntry () ; NavigableMap<K,V> descendingMap () ; NavigableSet<K> navigableKeySet () ; NavigableSet<K> descendingKeySet () ; NavigableMap<K,V> subMap (K fromKey, boolean fromInclusive, K toKey, boolean toInclusive) NavigableMap<K,V> headMap (K toKey, boolean inclusive) ; NavigableMap<K,V> tailMap (K fromKey, boolean inclusive) ; SortedMap<K,V> subMap (K fromKey, K toKey) ; SortedMap<K,V> headMap (K toKey) ; SortedMap<K,V> tailMap (K fromKey) ; }
注意:上述返回的map与原map是相互影响的
三、TreeMap的类定义 1 2 3 public class TreeMap <K ,V > extends AbstractMap <K ,V > implements NavigableMap <K ,V >, Cloneable , java .io .Serializable
实现NavigableMap接口,即能排序
实现了Cloneable接口,即覆盖了函数clone(),能克隆
实现了java.io.Serializable接口,意味着LinkedList支持序列化,能通过序列化去传输
四、TreeMap的属性 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 private final Comparator<? super K> comparator;private transient Entry<K,V> root;private transient int size = 0 ;private transient int modCount = 0 ;
五、TreeMap的构造函数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public TreeMap () comparator = null ; } public TreeMap (Comparator<? super K> comparator) this .comparator = comparator; } public TreeMap (Map<? extends K, ? extends V> m) comparator = null ; putAll(m); } public TreeMap (SortedMap<K, ? extends V> m) comparator = m.comparator(); try { buildFromSorted(m.size(), m.entrySet().iterator(), null , null ); } catch (java.io.IOException cannotHappen) { } catch (ClassNotFoundException cannotHappen) { } }
六、TreeMap的核心函数分析 1.put方法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 public V put (K key, V value) Entry<K,V> t = root; if (t == null ) { compare(key, key); root = new Entry<>(key, value, null ); size = 1 ; modCount++; return null ; } int cmp; Entry<K,V> parent; Comparator<? super K> cpr = comparator; if (cpr != null ) { do { parent = t; cmp = cpr.compare(key, t.key); if (cmp < 0 ) t = t.left; else if (cmp > 0 ) t = t.right; else return t.setValue(value); } while (t != null ); } else { if (key == null ) throw new NullPointerException(); @SuppressWarnings ("unchecked" ) Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; cmp = k.compareTo(t.key); if (cmp < 0 ) t = t.left; else if (cmp > 0 ) t = t.right; else return t.setValue(value); } while (t != null ); } Entry<K,V> e = new Entry<>(key, value, parent); if (cmp < 0 ) parent.left = e; else parent.right = e; fixAfterInsertion(e); size++; modCount++; return null ; }
2.以getEntry方法为基础的获取元素方法,containsKey()、get()、remove()等 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 final Entry<K,V> getEntry (Object key) if (comparator != null ) { return getEntryUsingComparator(key); } if (key == null ) { throw new NullPointerException(); } @SuppressWarnings ("unchecked" ) Comparable<? super K> k = (Comparable<? super K>) key; Entry<K,V> p = root; while (p != null ) { int cmp = k.compareTo(p.key); if (cmp < 0 ) { p = p.left; } else if (cmp > 0 ) { p = p.right; } else { return p; } } return null ; }
3.以getFirstEntry、getLastEntry为基础的获取头尾元素方法,其中包含firstKey、lastKey、firstEntry、lastEntry、pollFirstEntry、pollLastEntry 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 final Entry<K,V> getFirstEntry () Entry<K,V> p = root; if (p != null ) { while (p.left != null ) { p = p.left; } } return p; } final Entry<K,V> getLastEntry () Entry<K,V> p = root; if (p != null ) { while (p.right != null ) { p = p.right; } } return p; }
4.keySet()和entrySet() 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 @Override public Set<K> keySet () return navigableKeySet(); } @Override public NavigableSet<K> navigableKeySet () KeySet<K> nks = navigableKeySet; return (nks != null ) ? nks : (navigableKeySet = new KeySet<>(this )); } @Override public Set<Map.Entry<K,V>> entrySet() { EntrySet es = entrySet; return (es != null ) ? es : (entrySet = new EntrySet()); } class EntrySet extends AbstractSet <Map .Entry <K ,V >>
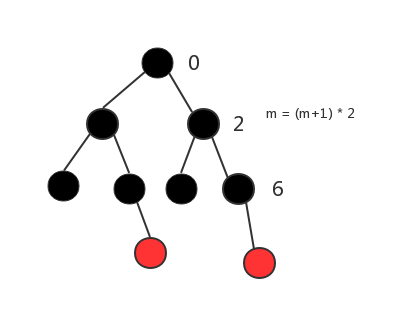
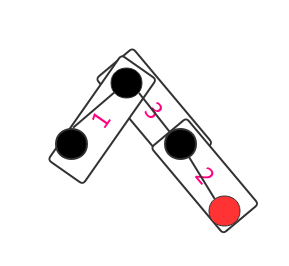
5.computeRedLevel 1 2 3 4 5 6 7 8 9 10 private static int computeRedLevel (int sz) int level = 0 ; for (int m = sz - 1 ; m >= 0 ; m = m / 2 - 1 ) { level++; } return level; }
构造树的完全二叉树的层数
6.buildFromSorted 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 @SuppressWarnings ("unchecked" )private final Entry<K,V> buildFromSorted (int level, int lo, int hi, int redLevel, Iterator<?> it, java.io.ObjectInputStream str, V defaultVal) throws java.io.IOException, ClassNotFoundException { if (hi < lo) return null ; int mid = (lo + hi) >>> 1 ; Entry<K,V> left = null ; if (lo < mid) left = buildFromSorted(level+1 , lo, mid - 1 , redLevel, it, str, defaultVal); K key; V value; if (it != null ) { if (defaultVal==null ) { Map.Entry<?,?> entry = (Map.Entry<?,?>)it.next(); key = (K)entry.getKey(); value = (V)entry.getValue(); } else { key = (K)it.next(); value = defaultVal; } } else { key = (K) str.readObject(); value = (defaultVal != null ? defaultVal : (V) str.readObject()); } Entry<K,V> middle = new Entry<>(key, value, null ); if (level == redLevel) middle.color = RED; if (left != null ) { middle.left = left; left.parent = middle; } if (mid < hi) { Entry<K,V> right = buildFromSorted(level+1 , mid+1 , hi, redLevel, it, str, defaultVal); middle.right = right; right.parent = middle; } return middle; }
buildFromSorted能这么构造是因为这是一个已经排序的map
七、TreeMap的内部类 1.keySet类 keySet继承于AbstractSet;实现了Set接口
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 static final class KeySet <E > extends AbstractSet <E > implements NavigableSet <E > private final NavigableMap<E, ?> m; KeySet(NavigableMap<E,?> map) { m = map; } @Override public Iterator<E> iterator () if (m instanceof TreeMap) { return ((TreeMap<E,?>)m).keyIterator(); } else { return ((NavigableSubMap<E,?>)m).keyIterator(); } } @Override public Iterator<E> descendingIterator () if (m instanceof TreeMap) { return ((TreeMap<E,?>)m).descendingKeyIterator(); } else { return ((NavigableSubMap<E,?>)m).descendingKeyIterator(); } } @Override public int size () return m.size(); } @Override public boolean isEmpty () return m.isEmpty(); } @Override public boolean contains (Object o) return m.containsKey(o); } @Override public void clear () @Override public E lower (E e) return m.lowerKey(e); } @Override public E floor (E e) return m.floorKey(e); } @Override public E ceiling (E e) return m.ceilingKey(e); } @Override public E higher (E e) return m.higherKey(e); } @Override public E first () return m.firstKey(); } @Override public E last () return m.lastKey(); } @Override public Comparator<? super E> comparator() { return m.comparator(); } @Override public E pollFirst () Map.Entry<E,?> e = m.pollFirstEntry(); return (e == null ) ? null : e.getKey(); } @Override public E pollLast () Map.Entry<E,?> e = m.pollLastEntry(); return (e == null ) ? null : e.getKey(); } @Override public boolean remove (Object o) int oldSize = size(); m.remove(o); return size() != oldSize; } @Override public NavigableSet<E> subSet (E fromElement, boolean fromInclusive, E toElement, boolean toInclusive) return new KeySet<>(m.subMap(fromElement, fromInclusive, toElement, toInclusive)); } @Override public NavigableSet<E> headSet (E toElement, boolean inclusive) return new KeySet<>(m.headMap(toElement, inclusive)); } @Override public NavigableSet<E> tailSet (E fromElement, boolean inclusive) return new KeySet<>(m.tailMap(fromElement, inclusive)); } @Override public SortedSet<E> subSet (E fromElement, E toElement) return subSet(fromElement, true , toElement, false ); } @Override public SortedSet<E> headSet (E toElement) return headSet(toElement, false ); } @Override public SortedSet<E> tailSet (E fromElement) return tailSet(fromElement, true ); } @Override public NavigableSet<E> descendingSet () return new KeySet<>(m.descendingMap()); } @Override public Spliterator<E> spliterator () return keySpliteratorFor(m); } }
2.values类 values继承于AbstractCollection;继承于Collection,继承于Iterable
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Values extends AbstractCollection <V > @Override public Iterator<V> iterator () return new ValueIterator(getFirstEntry()); } @Override public int size () return TreeMap.this .size(); } @Override public boolean contains (Object o) return TreeMap.this .containsValue(o); } @Override public boolean remove (Object o) for (Entry<K,V> e = getFirstEntry(); e != null ; e = successor(e)) { if (valEquals(e.getValue(), o)) { deleteEntry(e); return true ; } } return false ; } @Override public void clear () TreeMap.this .clear(); } @Override public Spliterator<V> spliterator () return new ValueSpliterator<K,V>(TreeMap.this , null , null , 0 , -1 , 0 ); } }
3.EntrySet 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 class EntrySet extends AbstractSet <Map .Entry <K ,V >> @Override public Iterator<Map.Entry<K,V>> iterator() { return new EntryIterator(getFirstEntry()); } @Override public boolean contains (Object o) if (!(o instanceof Map.Entry)) { return false ; } Map.Entry<?,?> entry = (Map.Entry<?,?>) o; Object value = entry.getValue(); Entry<K,V> p = getEntry(entry.getKey()); return p != null && valEquals(p.getValue(), value); } @Override public boolean remove (Object o) if (!(o instanceof Map.Entry)) { return false ; } Map.Entry<?,?> entry = (Map.Entry<?,?>) o; Object value = entry.getValue(); Entry<K,V> p = getEntry(entry.getKey()); if (p != null && valEquals(p.getValue(), value)) { deleteEntry(p); return true ; } return false ; } @Override public int size () return TreeMap.this .size(); } @Override public void clear () TreeMap.this .clear(); } @Override public Spliterator<Map.Entry<K,V>> spliterator() { return new EntrySpliterator<K,V>(TreeMap.this , null , null , 0 , -1 , 0 ); } }
4.Entry节点类 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 static final class Entry <K ,V > implements Map .Entry <K ,V > K key; V value; Entry<K,V> left; Entry<K,V> right; Entry<K,V> parent; boolean color = BLACK; Entry(K key, V value, Entry<K,V> parent) { this .key = key; this .value = value; this .parent = parent; } @Override public K getKey () return key; } @Override public V getValue () return value; } @Override public V setValue (V value) V oldValue = this .value; this .value = value; return oldValue; } @Override public boolean equals (Object o) if (!(o instanceof Map.Entry)) { return false ; } Map.Entry<?,?> e = (Map.Entry<?,?>)o; return valEquals(key,e.getKey()) && valEquals(value,e.getValue()); } @Override public int hashCode () int keyHash = (key==null ? 0 : key.hashCode()); int valueHash = (value==null ? 0 : value.hashCode()); return keyHash ^ valueHash; } @Override public String toString () return key + "=" + value; } }
八、TreeMap的遍历 Map没有迭代器,要将Map转化为Set,用Set的迭代器才能进行元素迭代
先通过entrySet()或ketSet()或values()方法获得相应的集合
通过Iterator迭代器遍历上面得到的集合
1.遍历TreeMap的Entry 1 2 3 4 5 6 7 8 9 10 11 Integer integ = null ; Iterator iter = map.entrySet().iterator(); while (iter.hasNext()) { Map.Entry entry = (Map.Entry)iter.next(); key = (String)entry.getKey(); integ = (Integer)entry.getValue(); }
2.遍历TreeMap的key 1 2 3 4 5 6 7 8 9 10 11 String key = null ; Integer integ = null ; Iterator iter = map.keySet().iterator(); while (iter.hasNext()) { key = (String)iter.next(); integ = (Integer)map.get(key); }
3.遍历TreeMap的value 1 2 3 4 5 6 7 8 Integer value = null ; Collection c = map.values(); Iterator iter= c.iterator(); while (iter.hasNext()) { value = (Integer)iter.next(); }